Herzog–Schönheim conjecture
In mathematics, the Herzog–Schönheim conjecture is a combinatorial problem in the area of group theory, posed by Marcel Herzog and Jochanan Schönheim in 1974.[1]
Let  be a group, and let
be a group, and let
be a finite system of left cosets of subgroups  of
of  .
.
Herzog and Schönheim conjectured that if  forms a partition of
forms a partition of  with
with 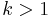 , then the (finite) indices
, then the (finite) indices ![[G:G_1],\ldots,[G:G_k]](/2012-wikipedia_en_all_nopic_01_2012/I/e00a04bc9dc3daf7c4cdddb8a170caed.png) cannot be distinct. In contrast, if repeated indices are allowed, then partitioning a group into cosets is easy: if
cannot be distinct. In contrast, if repeated indices are allowed, then partitioning a group into cosets is easy: if  is any subgroup of
is any subgroup of  with index
with index ![k=[G:H]<\infty](/2012-wikipedia_en_all_nopic_01_2012/I/e6b81ce5b412edb9b99fd6cf85696e95.png) then
then  can be partitioned into
can be partitioned into  left cosets of
left cosets of  .
.
Subnormal subgroups
In 2004 Zhi-Wei Sun proved an extended version of the Herzog–Schönheim conjecture in the case where  are subnormal in
are subnormal in  .[2] A basic lemma in Sun's proof states that if
.[2] A basic lemma in Sun's proof states that if  are subnormal and of finite index in
are subnormal and of finite index in  , then
, then
and hence
where 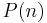 denotes the set of prime divisors of
denotes the set of prime divisors of  .
.
Mirsky–Newman theorem
When  is the additive group
is the additive group 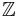 of integers, the cosets of
of integers, the cosets of  are the arithmetic progressions. In this case, the Herzog–Schönheim conjecture states that every covering system, a family of arithmetic progressions that together cover all the integers, must either cover some integers more than once or include at least one pair of progressions that have the same difference as each other. This result was conjectured in 1950 by Paul Erdős and proved soon thereafter by Leon Mirsky and Donald J. Newman. However, Mirsky and Newman never published their proof. The same proof was also found independently by Harold Davenport and Richard Rado.[3]
are the arithmetic progressions. In this case, the Herzog–Schönheim conjecture states that every covering system, a family of arithmetic progressions that together cover all the integers, must either cover some integers more than once or include at least one pair of progressions that have the same difference as each other. This result was conjectured in 1950 by Paul Erdős and proved soon thereafter by Leon Mirsky and Donald J. Newman. However, Mirsky and Newman never published their proof. The same proof was also found independently by Harold Davenport and Richard Rado.[3]
In 1970, a geometric coloring problem equivalent to the Mirsky–Newman theorem was given in the Soviet mathematical olympiad: suppose that the vertices of a regular polygon are colored in such a way that every color class itself forms the vertices of a regular polygon. Then, there exist two color classes that form congruent polygons.[3]
References
- ^ Herzog, M.; Schönheim, J. (1974), "Research problem No. 9", Canadian Mathematical Bulletin 17: 150. As cited by Sun (2004).
- ^ Sun, Zhi-Wei (2004), "On the Herzog-Schönheim conjecture for uniform covers of groups", Journal of Algebra 273 (1): 153–175, arXiv:math/0306099, doi:10.1016/S0021-8693(03)00526-X, MR2032455.
- ^ a b Soifer, Alexander (2008), "Chapter 1. A story of colored polygons and arithmetic progressions", The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators, New York: Springer, pp. 1–9, ISBN 978-0387746401.
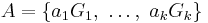
![\bigg[G:\bigcap_{i=1}^kG_i\bigg]\ \bigg|\ \prod_{i=1}^k[G:G_i]](/2012-wikipedia_en_all_nopic_01_2012/I/ae5e40b35062d7989554f0866fe60888.png)
![P\bigg(\bigg[G:\bigcap_{i=1}^kG_i\bigg]\ \bigg)
=\bigcup_{i=1}^kP([G:G_i]),](/2012-wikipedia_en_all_nopic_01_2012/I/d7121b5b8dffe9453832f2f95478e179.png)